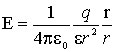Для объяснения природы электрических взаимодействий заряженных тел допускается наличие в окружающем заряды пространстве физического поля, осуществляющего это взаимодействие. В таком поле силовые взаимодействия между телами осуществляются через особую материальную среду, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью. Электрическое поле создается как неподвижными, так и движущимися зарядами. Наличие электрического поля оказывает силовое действие на движущиеся и неподвижные электрические заряды. Такое поле способно индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Термин «электрическое поле» первым внес в физику М. Фарадей – это особый вид материи, существующий вокруг любого электрического заряда и проявляющий себя в действии на другие заряды .

Таким образом, в физике создаваемое неподвижными электрическими зарядами поле принято называть электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся произвольным образом относительно системы отсчета.

Количественной характеристикой силового действия электрического поля на заряженные тела является напряжённостью электрического поля: E = F / q _пр . Напряженность поля определяется отношением силы F , действующей со стороны поля на точечный «пробный заряд» q _пр , помещенный в рассматриваемую точку поля, к величине этого заряда.

Закон Кулона позволил определить выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда: 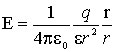_. Здесь r – радиус-вектор, соединяющий заряды q и q _пр .

Напряжённость поля точечного заряда во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

По­пы­та­ем­ся те­перь оха­рак­те­ри­зо­вать элек­тро­ста­ти­че­ское поле несколь­ких за­ря­дов. В этом слу­чае необ­хо­ди­мо вос­поль­зо­вать­ся сло­же­ни­ем век­тор­ных ве­ли­чин на­пря­жен­но­стей всех за­ря­дов. Вне­сем понятие «проб­ный заряд» и за­пи­шем сумму век­то­ров сил, дей­ству­ю­щих на этот заряд. Ре­зуль­ти­ру­ю­щее зна­че­ние на­пря­жен­но­сти по­лу­чит­ся при раз­де­ле­нии зна­че­ний этих сил на ве­ли­чи­ну проб­но­го за­ря­да. Дан­ный метод на­зы­ва­ет­ся прин­ци­пом су­пер­по­зи­ции [3-4] .

Напряжённость поля, создаваемого системой неподвижных точечных зарядов q ₁ , q ₂ , q ₃ , …, q _n , равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности (принцип суперпозиции):
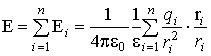. Здесь r _i – расстояние между зарядом q _i и рассматриваемой точкой поля.

Принцип суперпозиции [3-4], позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в проводнике, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq .

Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. На чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями [1-2].

Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление. С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого плотность силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности. Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.

Отметим важные свойства силовых линий:

- начинаются на положительных и заканчиваются на отрицательных зарядах;

- ее пересекаются;

- плотность линий тем больше, чем больше напряженность;

- напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности.

Графическое изоб­ра­жение на­пря­жен­ности элек­тро­ста­ти­че­ско­го поля си­ло­выми линиями иногда называют « ли­ни­я­ми на­пря­жен­но­сти» [8]. Такое изоб­ра­же­ние можно по­лу­чить, по­стро­ив век­то­ра на­пря­жен­но­сти поля в как можно боль­шем ко­ли­че­стве точек вб­ли­зи дан­но­го за­ря­да или целой си­сте­мы за­ря­жен­ных тел (рисунок 1.1).

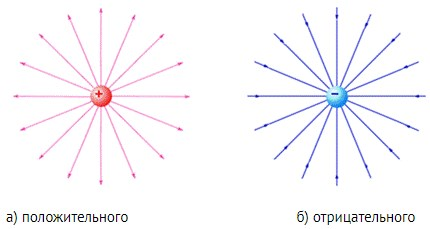
Рисунок 1.1. Линии на­пря­жен­но­сти элек­три­че­ско­го поля

то­чеч­но­го за­ря­да

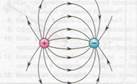
Рас­смот­рим несколь­ко при­ме­ров изоб­ра­же­ния си­ло­вых линий. Линии на­пря­жен­но­сти вы­хо­дят из по­ло­жи­тель­но­го за­ря­да (рисунок 1.1, а), то есть по­ло­жи­тель­ный заряд яв­ля­ет­ся ис­точ­ни­ком си­ло­вых линий. За­кан­чи­ва­ют­ся линии на­пря­жен­но­сти на от­ри­ца­тель­ном за­ря­де (рисунок 1.1, б).

Если проводник со­сто­ит из по­ло­жи­тель­но­го и от­ри­ца­тель­но­го за­ря­да и на­хо­дя­тся на ко­неч­ном рас­сто­я­нии друг от друга, линии напряженности между зарядами обозначаются как на рисунке 1.2, а. В этом слу­чае линии на­пря­жен­но­сти на­прав­ле­ны от по­ло­жи­тель­но­го за­ря­да к от­ри­ца­тель­но­му заряду.

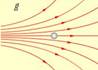
Боль­шой ин­те­рес пред­став­ля­ет элек­три­че­ское поле между двумя бес­ко­неч­ны­ми плос­ко­стя­ми. Если одна из пла­стин за­ря­же­на по­ло­жи­тель­но, а дру­гая от­ри­ца­тель­но, то в за­зо­ре между плос­ко­стя­ми со­зда­ет­ся од­но­род­ноеэлек­тро­ста­ти­че­ское поле, линия на­пря­жен­но­сти ко­то­ро­го ока­зы­ва­ют­ся па­рал­лель­ны­ми друг другу (рисунок 1.2, б).

а                               б                               в

Рисунок 1.2. Линии на­пря­жен­но­сти поля между двумя за­ря­дами (а)

и заряженными пластинами (б, в)

В слу­чае неод­но­род­но­гоэлек­три­че­ско­го поля ве­ли­чи­на на­пря­жен­но­сти опре­де­ля­ет­ся плотностью си­ло­вых линий: там, где си­ло­вые линии плотнее друг другу, ве­ли­чи­на на­пря­жен­но­сти поля боль­ше (рисунок 1.2, в).

Таким образом, ли­ни­я­ми на­пря­жен­но­сти на­зы­ва­ют непре­рыв­ные линии, ка­са­тель­ные к ко­то­рым в каж­дой точке сов­па­да­ют с век­то­ра­ми на­пря­жен­но­сти в этой точке. Линии на­пря­жен­но­сти яв­ля­ют­ся непре­рыв­ны­ми, на­чи­на­ют­ся на по­ло­жи­тель­ных за­ря­дах и за­кан­чи­ва­ют­ся на от­ри­ца­тель­ных зарядах.

Закон Ку­ло­на при­ме­ним толь­ко для то­чеч­ных по­ко­я­щих­ся за­ря­дов, а также за­ря­жен­ных ша­ри­ков, сфер. На­пря­жен­ность же поз­во­ля­ет ха­рак­те­ри­зо­вать элек­три­че­ское поле вне за­ви­си­мо­сти от формы за­ря­жен­но­го тела, ко­то­рое это поле со­зда­ет.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу А . Эта работа при малом перемещении равна (рисунок 1.3):

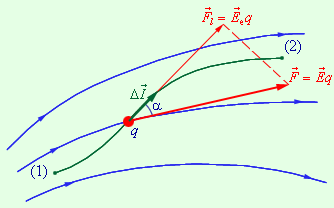
Рисунок 1.3. Работа электрических сил при малом перемещении заряда q

На рисунке 1.4 изображены силовые линии кулоновского поля точечного заряда q и две различные траектории перемещения пробного заряда из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение . Работа Δ A кулоновских сил на этом перемещении равна:

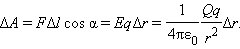
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δ r .

Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рисунке 1.4, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.

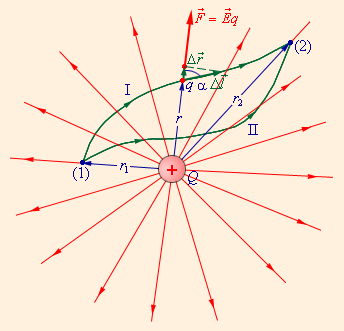
Рисунок 1.4. Работа кулоновских сил при перемещении заряда q

зависит только от расстояний r ₁ и r ₂ траектории

В разделе физики «Электростатика» энергию принято обозначать буквой W , так как буквой E обозначают напряженность поля. Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной нулевой точки. Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Потенциальная энергия заряда q , помещенного в электростатическое поле, пропорциональна величине этого заряда. Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом электрического поля: φ = W _p / q . Потенциал φ является энергетической характеристикой электростатического поля.

Во многих задачах электростатики при вычислении потенциалов за опорную нулевую точку удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность: φ _∞ = А _∞ / q .

Потенциал φ _∞ поля точечного заряда q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

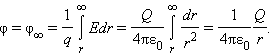
Эта формула выражает потенциал поля однородно заряженного шара при r ≥ R , где R – радиус шара. Для наглядного представления электростатического поля наряду с силовыми линиями используют «эквипотенциальные» поверхности (рисунок 1.5).

Таким образом, поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется «эквипотенциальной» поверхностью (поверхностью равного потенциала).

Силовые линии электростатического поля всегда перпендикулярны эквипотенциальным поверхностям. Значит, эквипотенциальные поверхности кулоновского поля точечного заряда являются концентрическими сферами. На рисунке 1.5 представлены картины силовых линий и «эквипотенциальных» поверхностей некоторых простых электростатических полей.

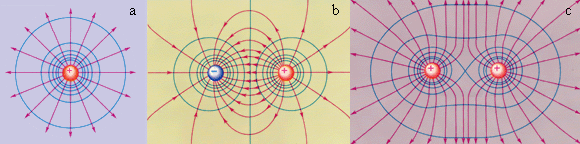
Рисунок 1.5. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции и для потенциалов: φ = φ ₁ + φ ₂ + φ ₃ + ...

Таким образом, потенциал поля является энергетической характеристикой поля и характеризует потенциальную энергию, которой обладал бы положительный единичный заряд, помещенный в данную точку поля: φ = W / q .