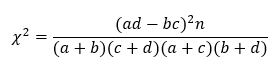
Существует множество признаков, различных явлений и вещей, измерение которых затруднено или вовсе невозможно. Например, как измерить признак «вид патологии» или «профессия», а как сравнить эти признаки для получения статистического представления о профессиональной заболеваемости?
В этих случаях изучается распространенность признаков, частота встречаемости признаков (доля объектов с интересующим нас признаком) в различных выборках, оценивается взаимосвязь частоты встречаемости одного признака с частотой встречаемости другого признака.
Для этого используются таблицы сопряженности. Столбцы этой таблицы обозначают градации одного признака, строки – градации другого признака. В каждой ячейке записывается число случаев с сопряженными признаками.
Наиболее простой случай таблица 2х2 (исследуется частота совместного распространения двух признака, каждый из которых имеет две градации). Еще их называют четырехпольными таблицами.
В общем случае Н(0) формулируется следующим образом:
СЛУЧАЙ 1. Выборки независимые
Предположим, что у нас есть два качественных признака, характеризующие обследованных лиц. Занесем эти данные в таблицу сопряженности
|
|
Первый признак (первая градация) | Первый признак (вторая градация) | Всего |
| Второй признак (первая градация) | Частота встречаемости a | Частота встречаемости b | a +b |
| Второй признак (вторая градация) | Частота встречаемости c | Частота встречаемости d | с+d |
| n 1 =a+c | n 2 =b+d | n=a+b+c+d |
Критерий хи-квадрат Пирсона вычисляется по формуле:
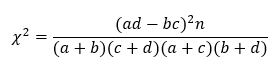
Но для таблицы 2х2 более точные результаты дает критерий с поправкой Йетса:
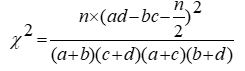
Его критическое значение находится для заданного уровня значимости
α
и числа степеней свободы
f
=
(
n
-1)(
m
-1),
где
n
и
m
число строк и число столбцов в таблице сопряженности
(
Приложение 5
).
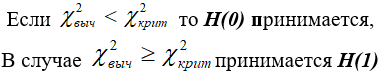
Когда число наблюдений невелико и в клетках таблицы встречается частота меньше 5, критерий хи-квадрат неприменим и для проверки гипотез используется точный критерий Фишера. Процедура вычисления этого критерия достаточно трудоемка и в этом случае лучше воспользоваться компьютерными программами статанализа.
По таблице сопряженности можно вычислить меру связи между двумя качественными признаками – ею является коэффициент ассоциации Юла Q (аналог коэффициента корреляции):
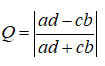
Q лежит в пределах от 0 до 1. Близкий к единице коэффициент свидетельствует о сильной связи между признаками. При равенстве его нулю – связь отсутствует.
Аналогично используется коэффициент фи-квадрат (φ 2 ):
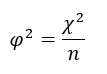
В примере с беременными, страдающими преэклампсией, была получена следующая таблица сопряженности:
| Преэклампсия есть | Преэклампсии нет | Всего в строке | |
| Ожирение есть | 120 (a) | 140 (b) | 260 |
| Ожирения нет | 332 (c) | 1520 (d) | 1852 |
| Всего в столбце | 452 | 1660 | 2112 |
Н(0): наличие у беременной выраженного ожирения не влияет на риск возникновения преэклампсии.
Н(1): наличие у беременной выраженного ожирения увеличивает риск возникновения преэклампсии.
Выберем уровень значимости: α=0,05.

Вывод: наличие у беременной выраженного ожирения статистически значимо (с вероятностью не менее 95%) увеличивает риск возникновения преэклампсии.
А теперь рассмотрим клиническую значимость влияния фактора ожирения на протекание беременности. Из таблицы сопряженности можно посчитать, что доля лиц с ожирением среди тех, у кого нет преэклампсии, составляет 140/1660*100%=8,4%. Среди лиц с преэклампсией эта доля 26,5%, разница составляет 18,1%. Это выборочная разница и для нее необходимо определить 95% доверительный интервал. Как это сделать мы уже рассматривали. После расчетов получаем, что генеральная разница лежит в пределах от 13,8% до 22,4%. Даже нижний предел ДИ свидетельствует о клинической значимости этих различий.
Коэффициент ассоциации Юла Q =0,6 указывает на среднюю по силе связь между фактором риска и предродовым осложнением.
Эти же данные, обработанные в программе STATISTICA (модуль «непараметрическая статистика, таблицы 2×2»).
| Столбец 1 | Столбец 2 | Всего | |
| Частоты, стро а 1 | 120 | 140 | 260 |
| % случаев | 5,7 % | 6,6 % | 12,3 % |
| Частоты, строка 2 | 332 | 1520 | 1852 |
| % случаев | 15,7 % | 72 % | 87,76 % |
| Всего | 452 | 1660 | 2112 |
| % всего | 21,4 % | 78,6 % | |
| Хи-квадрат (f=1) | 107,99 | p=0,0000 | |
| Поправка Йетса | 106,32 | p=0,0000 | |
| Фи-квадрат | ,05113 | ||
| Точный ритерий Фишера, одностор. | ---- | ||
| Точный критерий Фишера, двустор. | ---- | ||
| Хи-квадрат Макнемара | 1193,42 | p=0,0000 |
Таблицы сопряженности могут иметь и более сложный вид, когда каждый признак имеет более двух градаций. Нулевая гипотеза заключается в отсутствии связи между этими признаками. Ниже приведен пример подобного случая – нужно выяснить есть ли взаимосвязь между профессией и обращаемостью к врачу.
|
|
Профессия | всего | |||
| Обращаемость к врачу | строители | шахтеры | учителя | госслужащие | |
| до 3 в год | 21 | 26 | 19 | 17 | 83 |
| от 4 до 6 в год | 9 | 15 | 12 | 6 | 42 |
| более 6 в год | 7 | 8 | 6 | 4 | 25 |
| всего | 37 | 49 | 37 | 27 | 150 |
Анализ таких таблиц также предпочтительно проводить с использованием компьютерных программ.
СЛУЧАЙ 2. Выборки зависимые
Проблема. Острые респираторные вирусные инфекции (ОРВИ) являются серьезной проблемой здравоохранения во многих регионах мира в связи с их широкой распространенностью и наносимым ими значительным социально – экономическим ущербом. Исследования показали, что у 92-94 % детей, страдающих частыми респираторно-вирусными заболеваниями, имел место дисбактериоз кишечника. Наличие дисбаланса нормофлоры, снижая антиинфекционную резистентность организма ребенка, не только сопровождает, но и влияет на частоту и характер течения острой респираторной инфекции у детей, способствуя развитию осложнений, что и позволяет считать терапевтическое и профилактическое применение биологических препаратов целесообразным и патогенетически обоснованным.
Стояла задача изучить эффективность пробиотика метаболитного типа в комплексной терапии у детей при осложненной смешанной респираторной вирусной инфекции и его влияние на микробиоценоз кишечника. В исследовании приняли участие 32 больных в возрасте от 1 мес. до 13 лет со среднетяжелыми и тяжелыми осложненными формами ОРВИ. Были получены следующие данные.
Частота нарушений микрофлоры после лечения снизилась на 43,8-15,6=28,2%. Подтверждают ли результаты выборочного исследования эффективность пробиотика?
Над одними и теми же объектами проводятся два наблюдения: «до» и после. (прием лекарства, обучение, внушение и т.д.)
Подсчитывается сколько раз данное свойство встречается:
|
|
Признак «после» | |
| Признак «до» | Вторая градация «после» (-) | Первая градация «после» (+) |
| Первая градация «до» (+) | a Число изменений от (+) к (-) | b Число сохранивших (+) |
| Вторая градация «до» (-) | c Число сохранивших (-) | d Число изменений от (–) к (+) |
Н(0) – частота встречаемости градаций признака после воздействия фактора не изменилось.
Критерием для проверки нулевой гипотезы является хи-квадрат М акнемара:
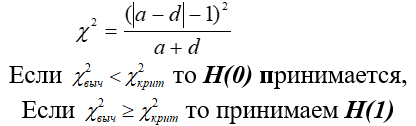
В задаче с эффективностью пробиотика составим следующую таблицу сопряженности для зависимых выборок. В ячейку a запишем число лиц, у которых был обнаружен дисбактериоз до лечения, но не обнаружен после (28,2% или 9 человек из 32). В ячейку b – число лиц, которым лечение не помогло (15,6% или 5 человек), в ячейку с – долю лиц, у которых как не было дисбактериоза, так и нет (56,2% или 18 человек), и в ячейку d – долю лиц, у которых после лечения вдруг он обнаружился (в нашем случае таких не было).
| До лечения пробиотиком | После лечения пробиотиком | |
| Нет дисбактериоза | Есть дисбактериоз | |
| Есть дисбактериоз | a 9 | b 5 |
| Нет дисбактериоза | c 18 | d 0 |
Н(0): частота нарушений микрофлоры кишечника не зависит от лечения пробиотиком.
Н(1): частота нарушений микрофлоры кишечника зависит от лечения пробиотиком.
Выберем уровень значимости: α=0,05, вычислим χ 2 = 7, 11.
Критическое значение = 3,841 (по таблице для f= 1, Приложение 5). Полученное значение χ 2 = 7,11 больше, чем критическое, следовательно, мы отвергаем нулевую гипотезу и принимаем альтернативную.
Вывод: с вероятностью не менее 95% частота нарушений микрофлоры кишечника зависит от лечения пробиотиком.
Определим 95%ДИ для разности долей, он составляет от 12,5 до 43,7%. Доверительный интервал достаточно широкий, т.е. доля лиц с положительны эффектом от лечения определена неточно, что может быть связано с недостаточным объемом выборки. Однако, даже нижний предел ДИ свидетельствует о клиническом эффекте от применения препарата.