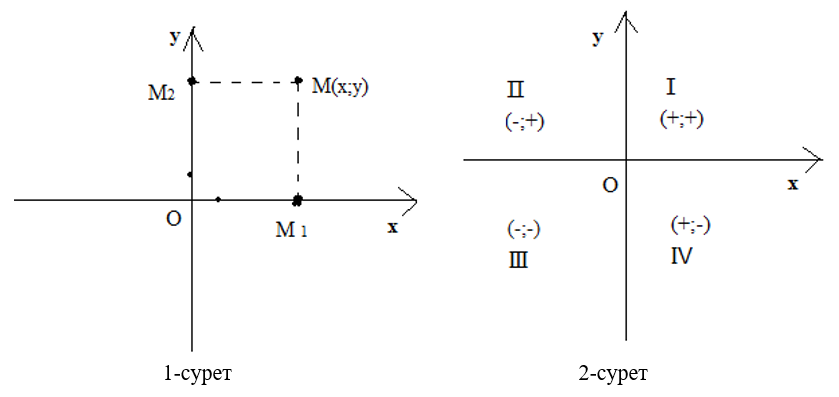
Тік бұрышты координаталар жүйесі мектеп курсынан белгілі. Жазықтықта координаталар жүйесін енгізу үшін өзара перпендикуляр екі түзу (екі ось) жүргізіп, олардың әрқайсысына бағыт беріп, кесінділердің өлшем бірлігін таңдау керек. Горизонталь, вертикаль орналасқан түзулер О нүктесенде қиылыссын. Горизонталь осьті х – деп белгілеп, оны абсциссаосі деп,ал вертикаль осьті у – деп белгілеп, ордината осі деп атаймыз. Олардың О - қиылысу нүктесін координаталар басы деп атайды.
Координаталар басы ортақ және масштаб бірлігі тең өзара перпендикуляр екі түзу (ось) тік бұрышты декарттық координаталар жүйесін немесе координаталық жазықтықты құрайды. Бұл жүйені хОу жүйесі деп белгелейміз.
Жазықтықта кез келган М нүкте алалық. Осы нүктеден координаталық осьтерге ММ 1 және ММ 2 перепендикулярларын түсірсек, М нүктесінің х осіндегі проекциясы М 1 нүктесі болады.
Осы сияқты М нүктесінің у осіне проекциясы М 2 нүктесі болады. Сонда ОМ 1 = х · е, ОМ 2 = у · е шарттарын қанағаттандыратын х, у сандарын табуға болады. Мұндағы е – бірлік кесінді (масштаб бірлігі).
Сонымен, егер жазықтықта кез келген М нүктесі берілсе, онда берілген координаталық жүйеде осы нүктеге сәйкес келетін х және у сандарының жұбын табуға болады және керісінше, егер х,у сандарының жұбы берілсе, онда берілген координаталық жүйеде осы сандар жұбына сәйкес М нүктесін табамыз. Мұндағы х саны М нүктесінің абсциссасы деп, ал у саны ординатасы деп аталады. М( х;у ) деп жазамыз (1-сурет).

Координаталық осьтер жазықтықты төрт бөлікке - I, II, III, IV ширектерге бөледі. Кооринаталардың таңбалары нүктесіне қай ширекте орналасқанына байланысыты өзгереді. 2- суретте таңбалардың өзгеруі көрсетілген.
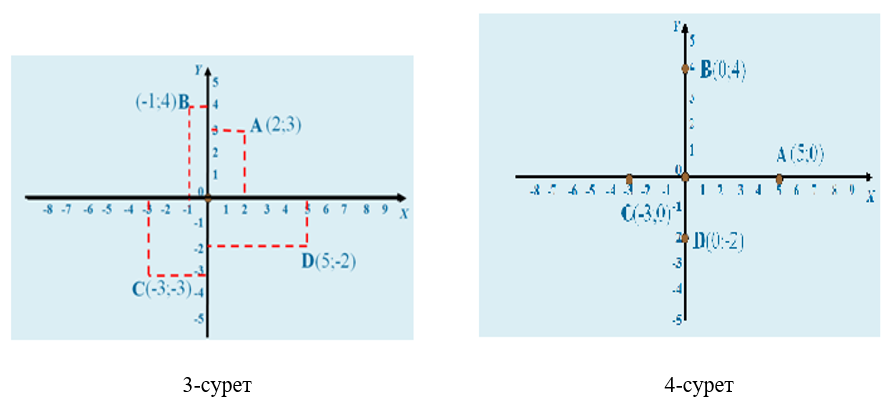
1-мысал . А(2;3), В(-1;4), С(-3;-3), D(5;-2) нүктелерін координаталық жазықтықта бейнелеу керек (3-сурет).
2-мысал . А(5;0), В(0;4), С(-3;0), D(0;-2) нүктелерін координаталық жазықтықта бейнелеу лкерек (4-сурет).
Координаталық жазықтықта А(х 1 ;у 1 ) және В(х 2 ;у 2 ) нүктелері берілсін (5-сурет). Берілген координаталары бойынша олардың ара қашықтығын анықталық. Ол үшін А және В нүктелерінен координаталық осьтерге перпендикулярлар жүргізіп, олардың қиылысуында С нүктесін аламыз. Шыққан АВС үшбұрышы – тікбұрышты үшбұрыш. Пифагор теоремасынан АВ² = АС² + СВ². Бірақ АС = А 1 В 1 = │х₂-х₁│, СВ = А 2 В 2 = │у₂-у₁│. Сондықтан
АВ² = (х 2 -х₁)² + (у₂-у₁)² (1)
Сонымен А және В нүктелерінің ара қашықтығы
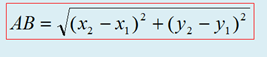
(2) формуласымен есептеледі.
Егер координаталар басы О(0;0) нүктесінен М(х;у) нүктесіне дейінгі қашықтықты табу керек болса, (1) формуладан
ОМ² = х²+у² (3)
Мысал . А(2;1) және В(5;3) нүктелерінің ара қашықтығын табу керек(6-сурет).
Шешуі . (1) формуладан АВ² = (5-2)² + (3-1)² = 9+4=13.
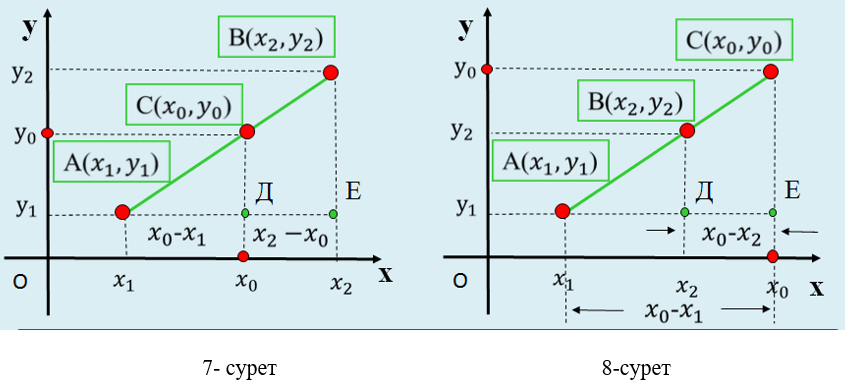
А(х 1 ; у 1 ), В(х 2 ;у 2 ) нүктелері және саны берілен болсын. С нүктесінің (х 0 ;у 0 ) координаталарын табу керек. А, В және С нүктелерін сәйкес Oх осіне және Oу осіне проекциялалық (7-сурет). Сонда AD = x 0 -x 1 , DE = х 2 -х 0 болады. Фалес теоремасынан
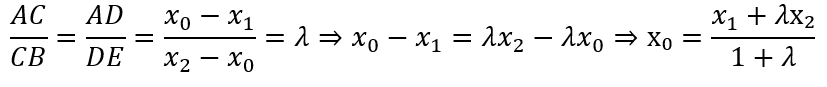
Осы сияқты
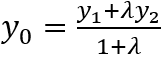 табамыз
табамыз
Сонымен С нүктесінің ізделінді координаталары
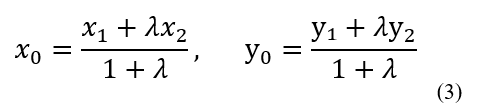 формулаларымен табылады.
формулаларымен табылады.
Ескерту! Егер С нүктесі АВ кесіндісінен тыс, бірақ АВ түзуінің бойында жатса, онда λ < 0 теріс сан болады (8-сурет).
Ескерту! Егер С нүктесі АВ кесіндісінің ортасы болса, онда λ=1 және (3)-дан
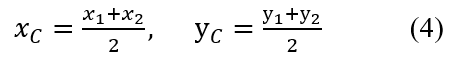
Координаталар көмегімен үшбұрыш ауданын есептеуге де болады. Айталық, АВС үшбұрышының төбелерінің координаталары белгілі болсын: А(х 1 ;у 1 ), В(х 2 ;у 2 ), С(х 3 ;у 3 ). Бұл үшбұрыштың ауданын келесі формуламен есептей аламыз:
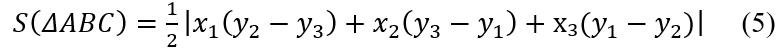
Немесе екінші ретті анықтауыш арқылы жазсақ:
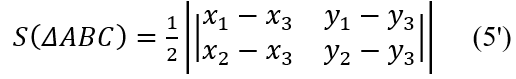
1 – мысал . Үшбұрыштың төбелері берілген: А(-1;-3), В(3;4), С(5;2). АВС үшбұрышының ауданын есептеу керек (9-сурет).
Шешуі . (5) формула бойынша
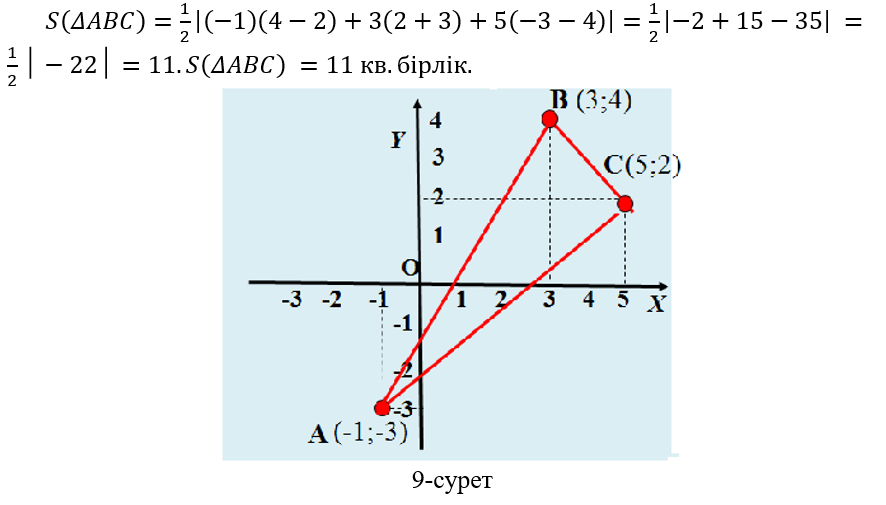
2 – мысал . Төртбүрыштың төбелеріберілген: А(0,3), В(4;0), С(6;2), D(4;7). ABCD төртбұрышының ауданын есептеу керек (10-сурет).
Шешуі . ABCD төртбұрышын екі ABD және BCD үшбұрышқа бөліп қарастырамыз. Үшбұрыштардың аудандарын жеке жеке есептеп қосып, ABCD төртбұрышының ауданын табамыз.
(5) формуладан:
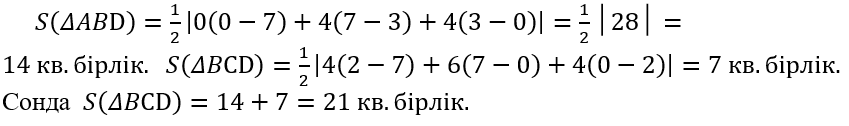
Осы әдіспен үшбұрыштарға бөлшектеу арқылы кез келген көпбұрыштың да ауданын есептеуге болады.