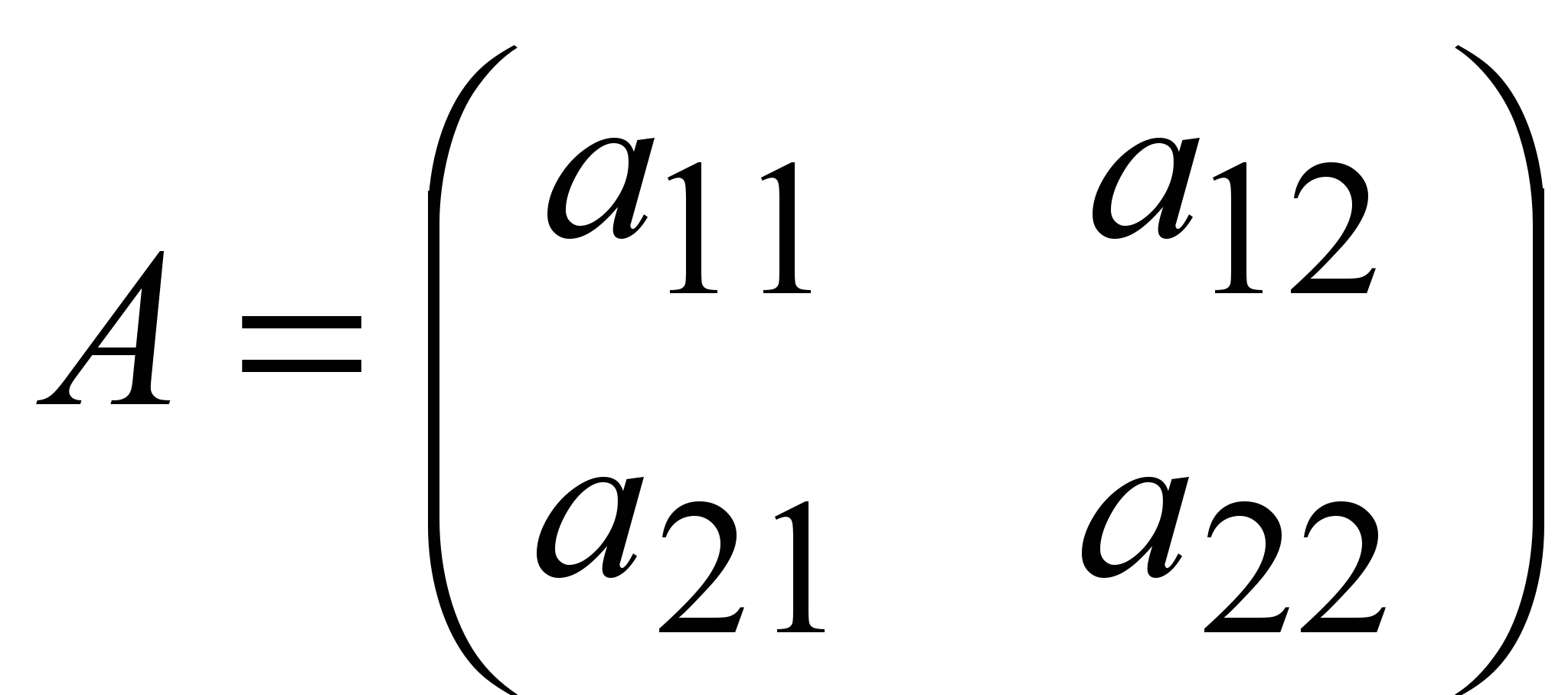матрицасы берілсін.
1.2.1.
Анықтауыштар.
Анықтауыштар жөніндегі ұғым, тек шаршы
(квадрат) матрицалар үшін ғана енгізіледі.
Айталық, екінші ретті шаршы
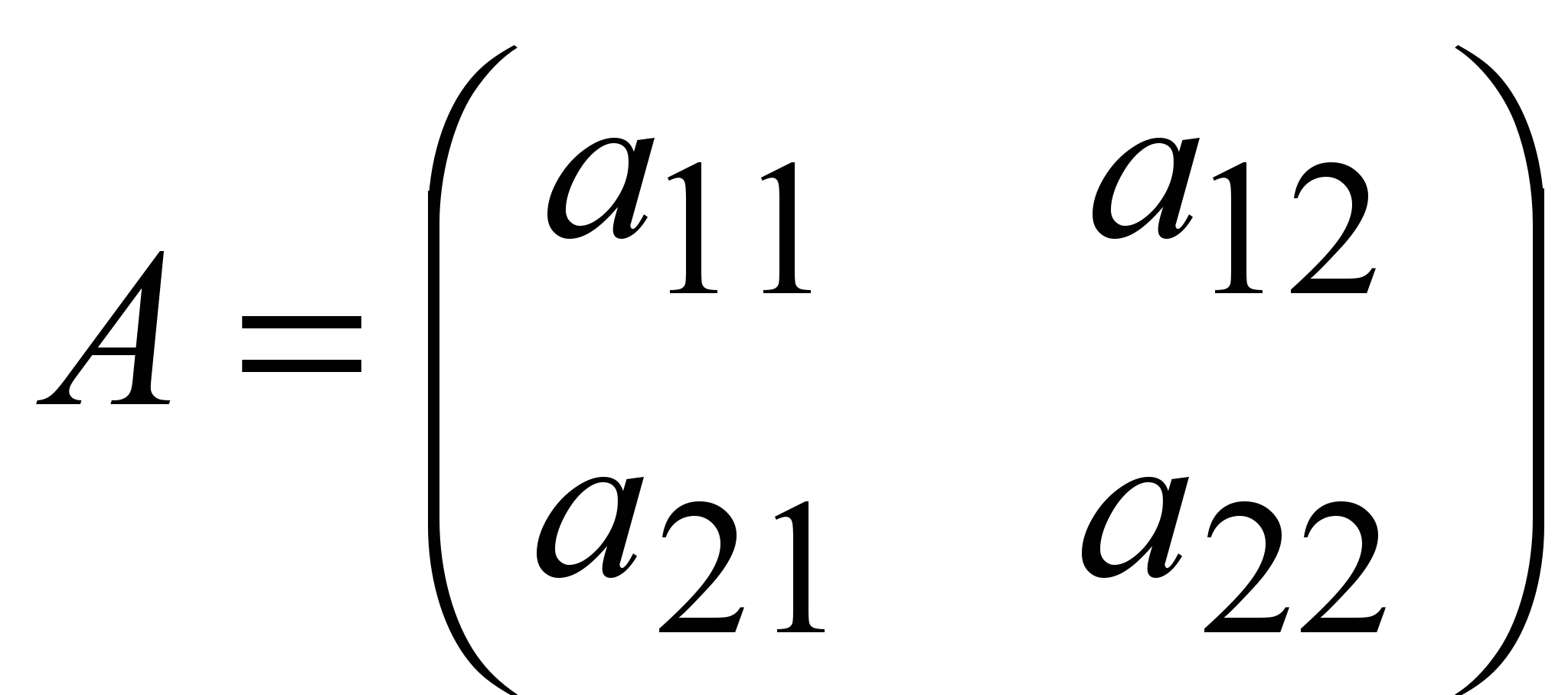матрицасы берілсін.
Берілген A матрицасының элементтері арқылы анықталған, диагональдар сүлбесі бойынша құрылған, a 11 a 22 -a 12 a 21 санын, екінші ретті анықтауыш (детерминант) деп атаймыз да,
Дәл осы сияқты, үшінші ретті шаршы матрица
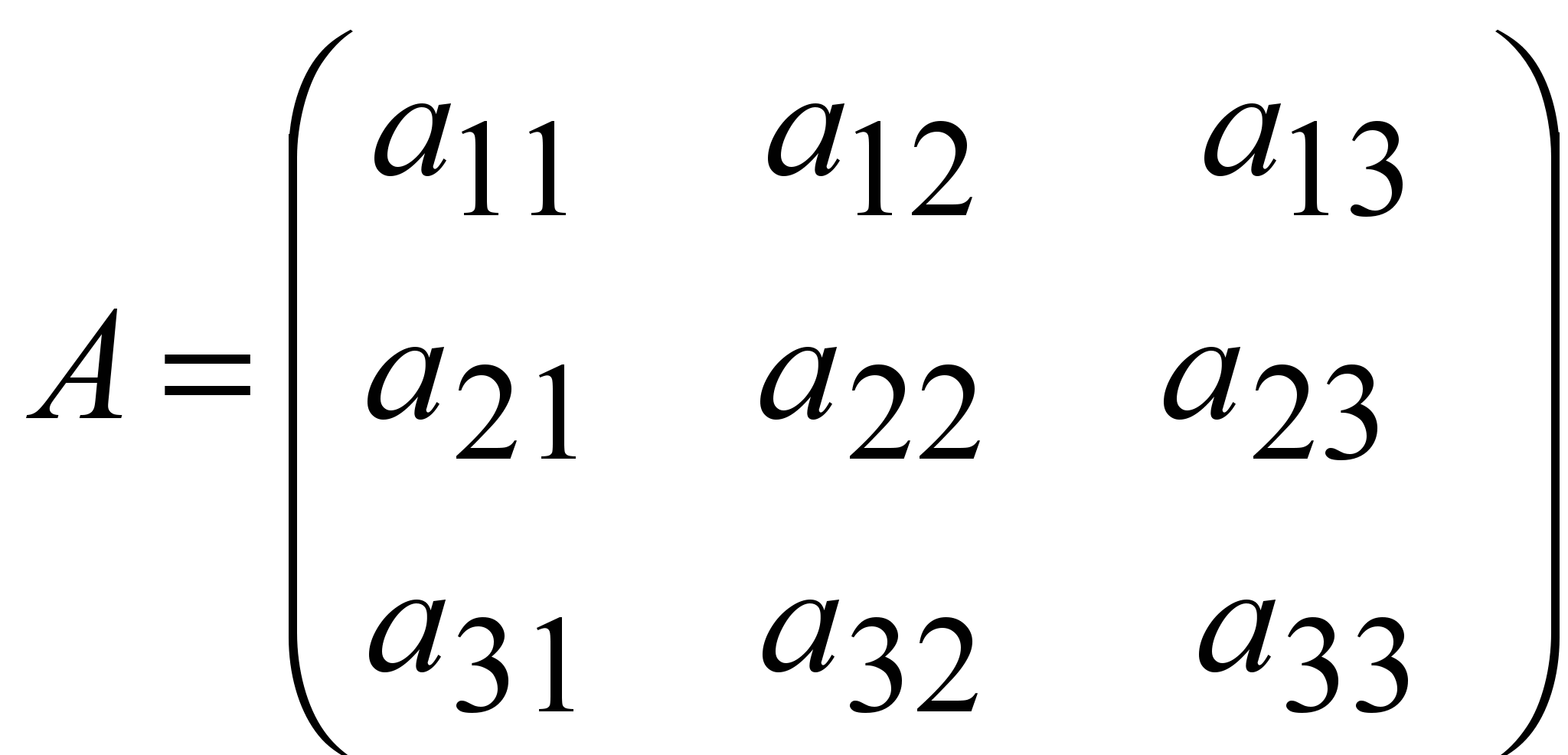берілсе, онда оған сәйкес алынған,
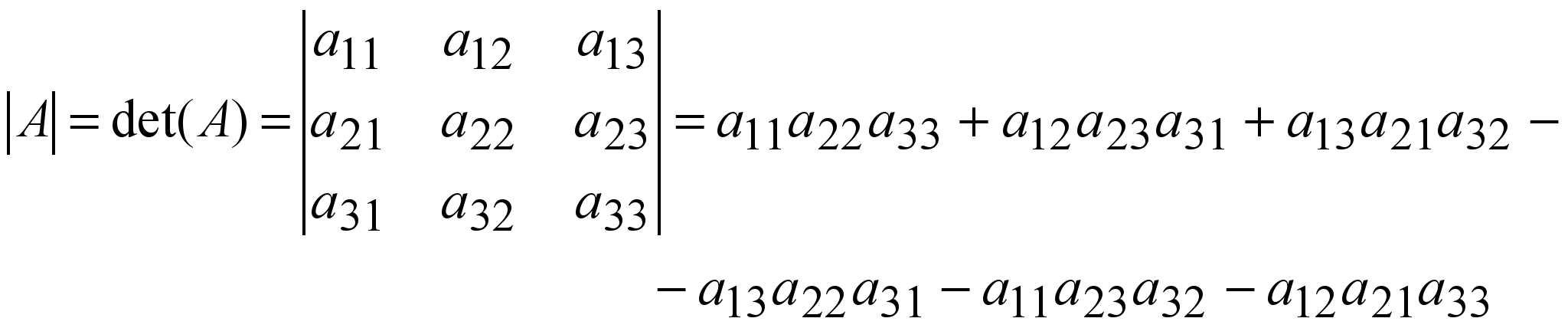(1.12)
саны, үшінші ретті анықтауыш (детерминант) деп аталады.
Бұл (1.12) теңдіктен, үшінші ретті анықтауышты есептеу үшін, жиі қолданылатын екі тәсілді атап өтейік.
1 o . Үшбұрыштар тәсілі (үшбұрыштар сүлбесі).
Келтірілген сүлбе бойынша, оң таңбамен алынған бас диагональ бойындағы элементтердің және табандары бас диагональға параллель, тең бүйірлі үшбұрыштардың төбелерінде орналасқан элементтердің көбейтінділері мен теріс таңбамен алынған, қосалқы диагональ бойындағы элементтердің және табандары осы диагональға параллель болатын тең бүйірлі үшбұрыштардың төбелерінде орналасқан элементтердің көбейтінділерінің қосындысына тең:
Бұдан сәйкес элементтердің көбейтінділерін құрап қосу арқылы (1.12) формуланы аламыз.
2 o . Саррюс сүлбесі.
Саррюс сүлбесі бойынша, берілген үшінші ретті анықтауыштың алғашқы екі бағанын косымша баған етіп бастапқы анықтауышқа тіркеп жазамыз. Енді: бас диагональ мен оған параллель болатын екі түзу бойында орналасқан элементтердің көбейтіндісін "+" − оң таңбамен, ал қосалқы диагональ мен оған параллель түзулер бойында орналасқан элементтердің көбейтінділерін "−" − теріс таңбамен алып, нәтижелерін қосамыз.
Ескерту. Жоғарыдағы (1.12) формуладан, үшінші ретті анықтауыштың 3!=6 − үш-үштен алынған элементар көбейтінділерден, ал оның әрбір мүшесі (қосылғышы) − әр жол мен әр бағаннан бір-бірден алынған элементтердің көбейтінділерінен тұратынын көреміз.
М.4*.
−
анықтауыштарды
есептейік.
Шешуі. Бірінші анықтауышты есептеу үшін, (1.11) − диагональдар сүлбесін пайдаланып, бас диагональ бойында орналасқан элементтердің көбейтінділеріне, қарама-қарсы таңбамен алынған қосалқы диагональ бойында орналасқан элементтердің көбейтіндісін қоссақ болғаны.
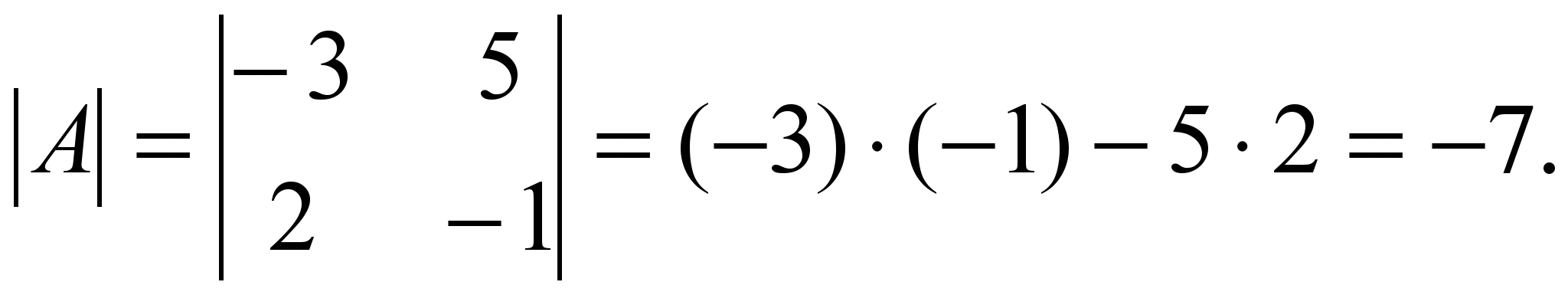
Екіншісін − үшбұрыштар немесе Саррюс сүлбелерін қолданып алынған (1.12) формула бойынша есептейміз:
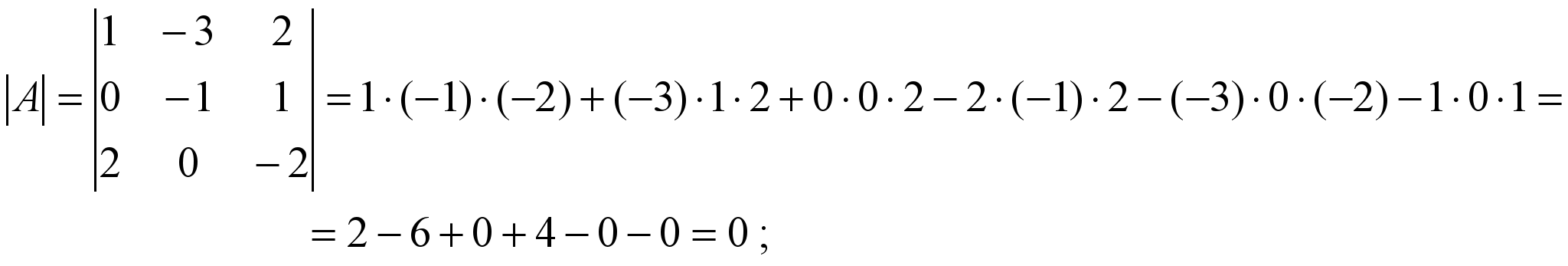
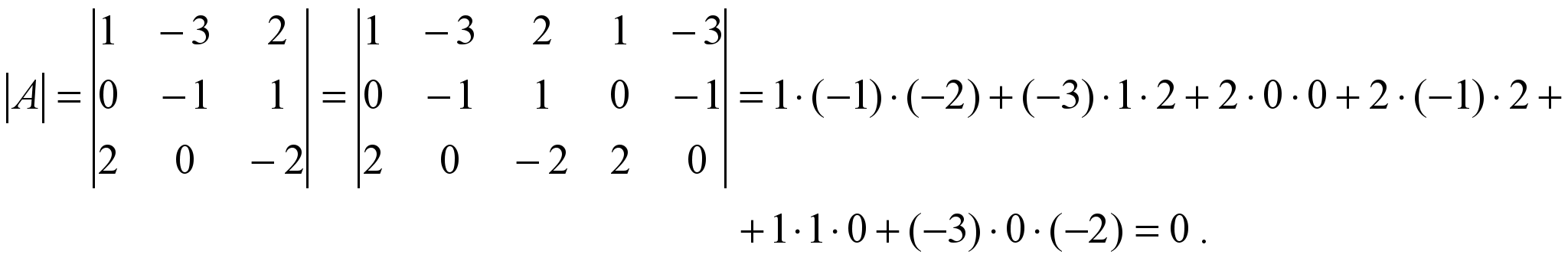
1.2.2. Анықтауыштардың қасиеттері. Ескеретін жағдай, кез келген ретті анықтауыштар үшін оның қасиеттері бірдей. Сондықтан біз тек үшінші ретті анықтауыштың қасиеттерін атап өтсек жеткілікті.
1 o . Анықтауышты транспонирлегеннен анықтауыштың мәні өзгермейді, яғни |A|-|A T |.
2 o . Анықтауыштың кез келген екі жолын (бағанын) ауыстырғаннан оның таңбасы қарама-қарсыға өзгереді.
3 o . Егер анықтауыштың кез келген бір жолының (бағанының) элементтері толығымен нөлге тең болса, онда анықтауыштың мәні де нөлге тең.
4 o . Анықтауыштың кез келген бір жолының (бағанының) ортақ көбейткішін оның алдына шығаруға болады,
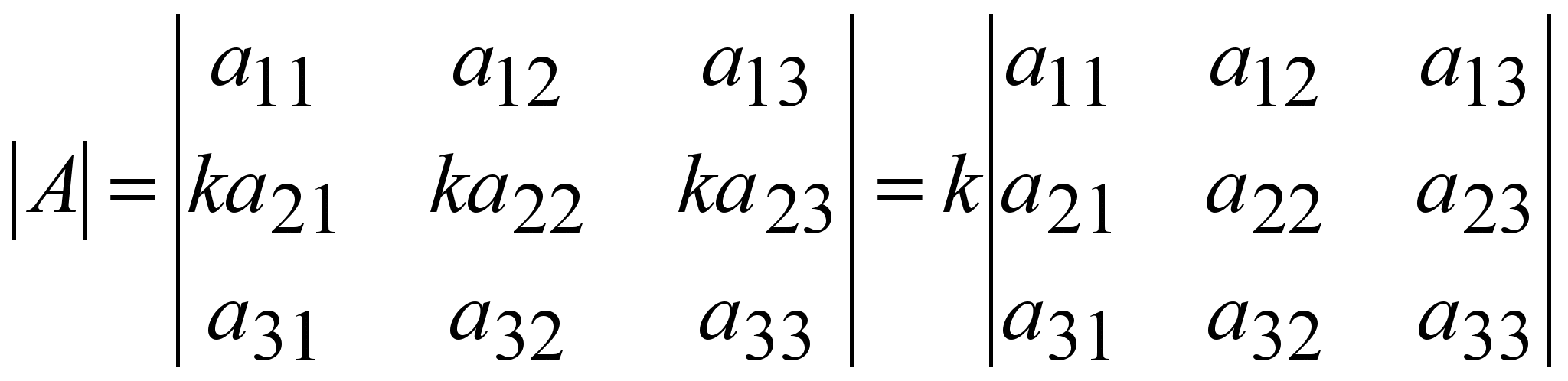(1.13)
5 o . Анықтауыштың кез келген екі жолының (бағанының) сәйкес элементтері өзара тең немесе прапорционал болса, ол анықтауыштың мәні нөлге тең.
6 o . Егер анықтауыштың кез келген i-жолының (j-бағанының) барлық элементтері қосыдыдан тұратын болса, онда анықтауыштың мәні қосылғыштардың қосындысына тең:
+
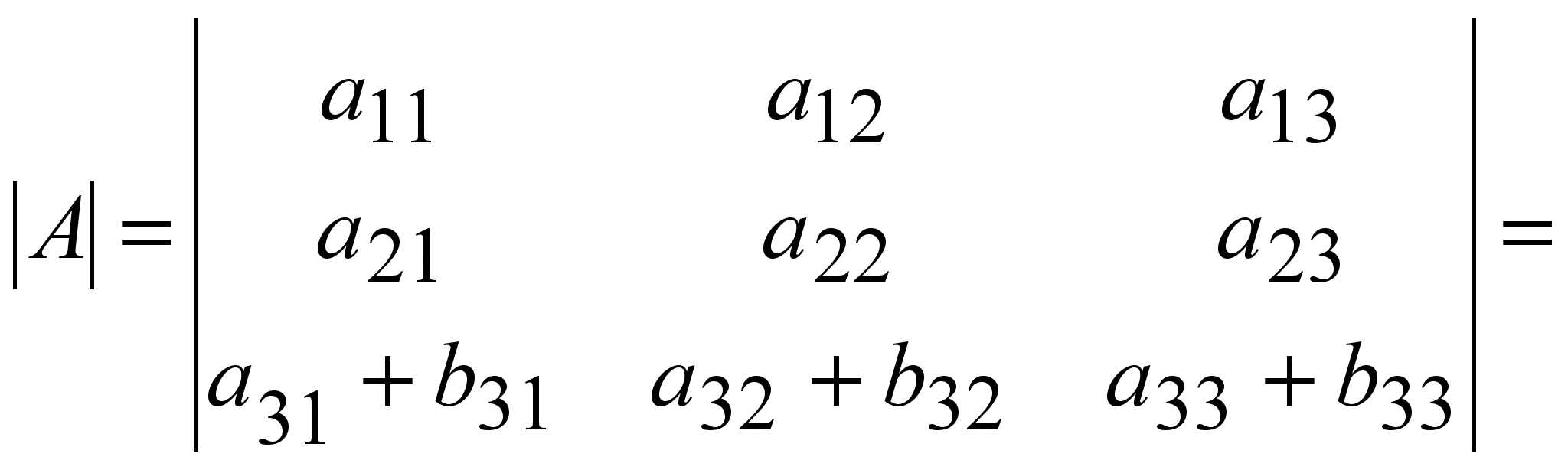
(1.14)
7 o . Анықтауыштың кез келген бір жолының (бағанының) элементтерін бірдей санға көбейтіп, басқа жолдың (бағанның) сәйкес элементтеріне қосқаннан анықтауыштың мәні өзгермейді,
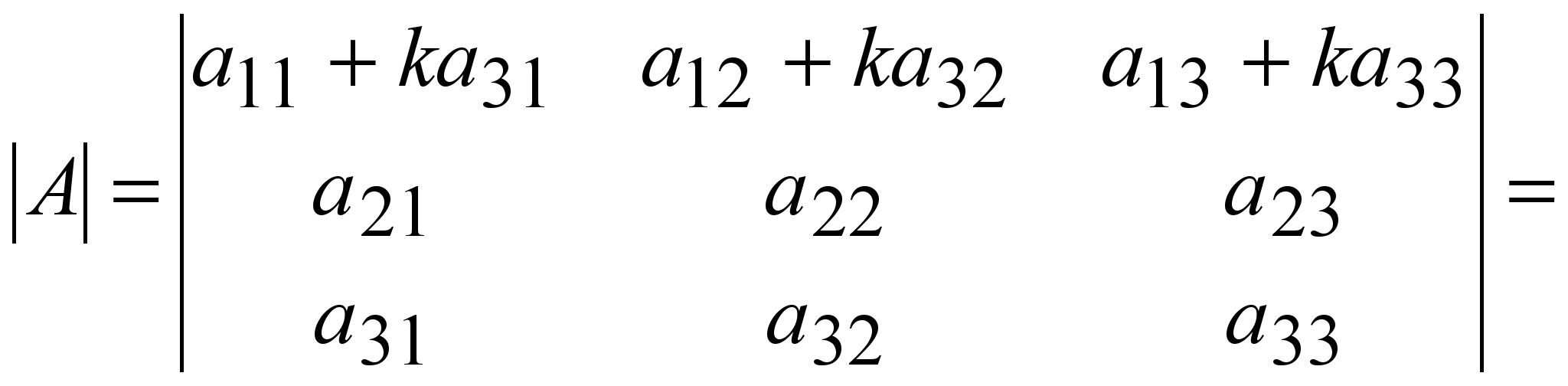
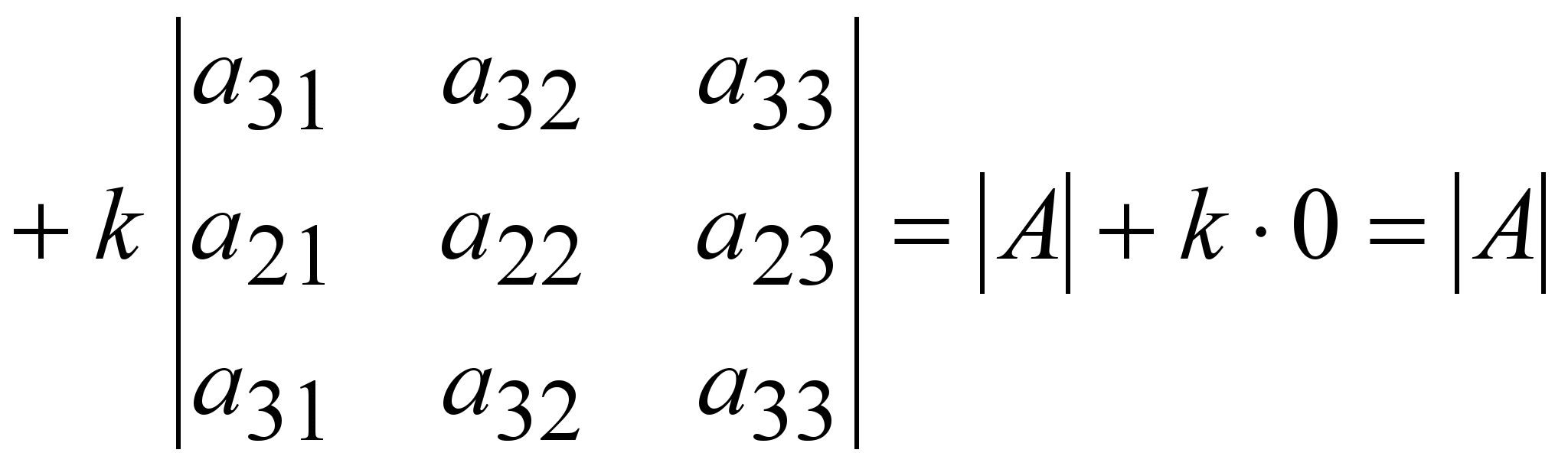
(4 o және 5 o қасиет бойынша).
Ескерту. 6 o және 7 o қасиеттерді баған бойынша да сәйкестендіріп жазуға болады.
Үшінші
ретті анықтауыштың кез келген бір жолы
мен бір бағанында орналасқан элементтерді
өзара перпендикуляр түзулермен сызып,
қалған элементтерден екінші ретті
анықтауыш құрсақ (мысал үшін,
2-ші
жолы мен
3-ші
бағанының), пайда болған жаңа анықтауыш
−
,
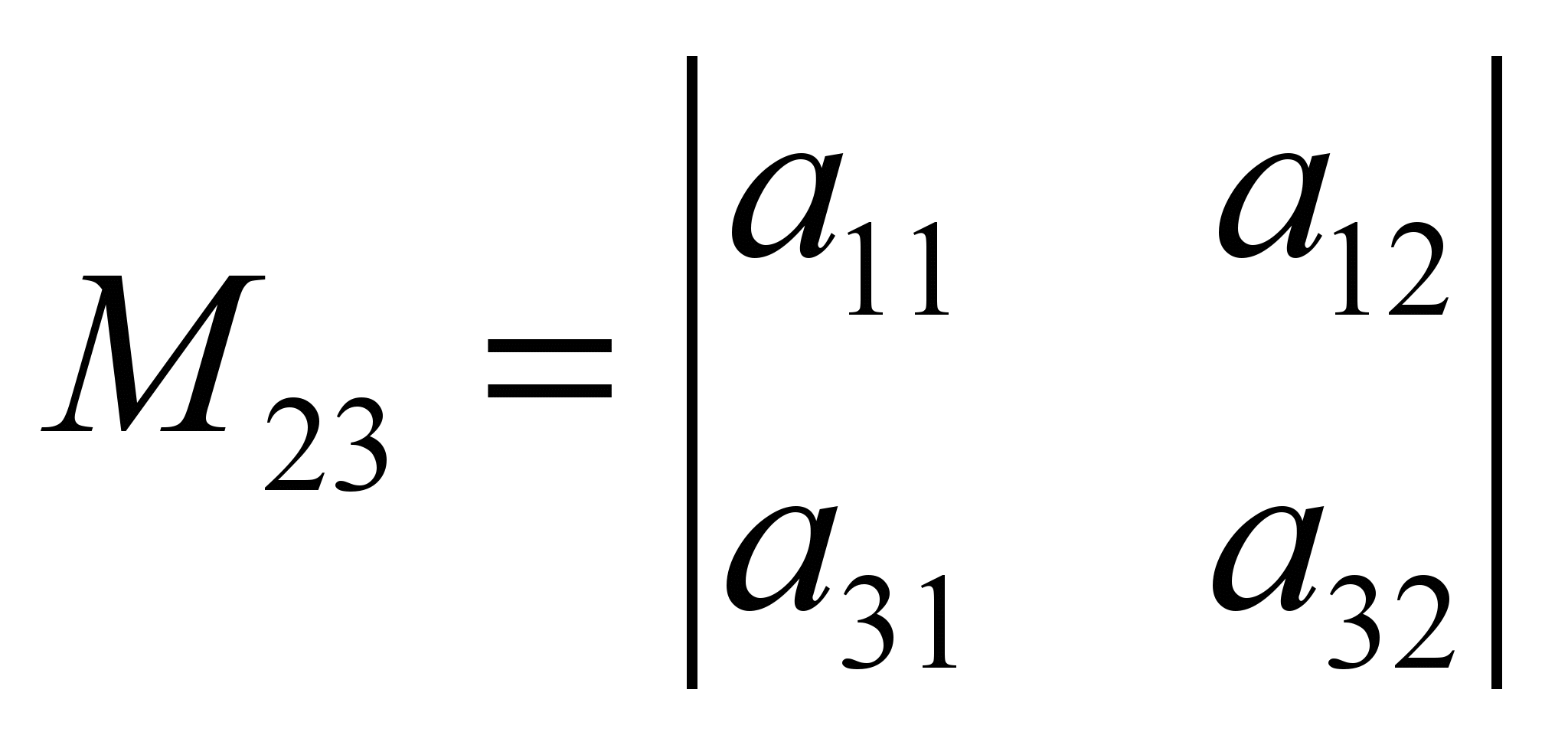берілген анықтауыштың
a
23
элементіне сәйкес
миноры
деп
аталады. Дәл осы сияқты кез келген
a
ij
, i=1,2,3; j-1,2,3
элементтері үшін сәйкес минорлар құруға
болады.
Анықтауыштың а ij элементінің алгебралық толықтауышы деп,
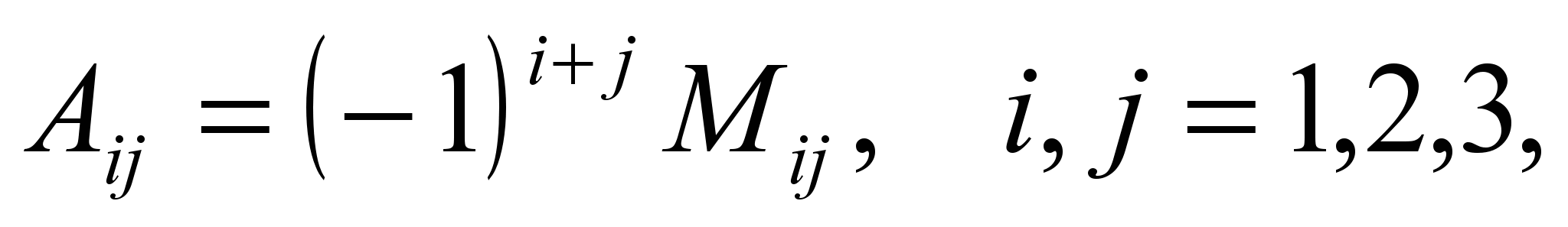(1.15)
санын
айтамыз. Мысал үшін,
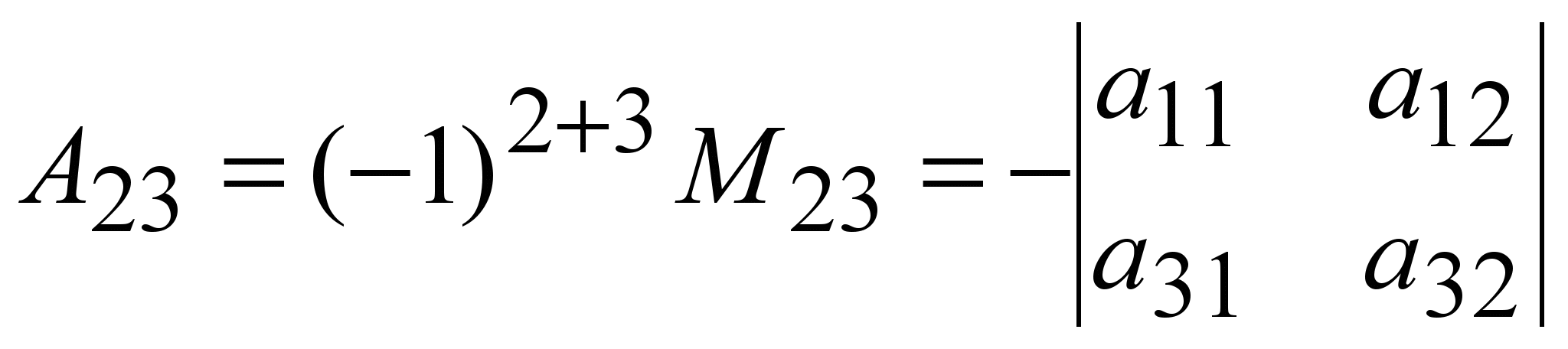санына тең.
Минорлар мен алгебралық толықтауыштарды пайдаланып, анықтауыштың келесі қасиеттерін келтірейік.
8 o . Кез келген жолдың (бағанның) элементтері мен, сол элементтерге сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы берілген анықтауыштың мәніне тең,
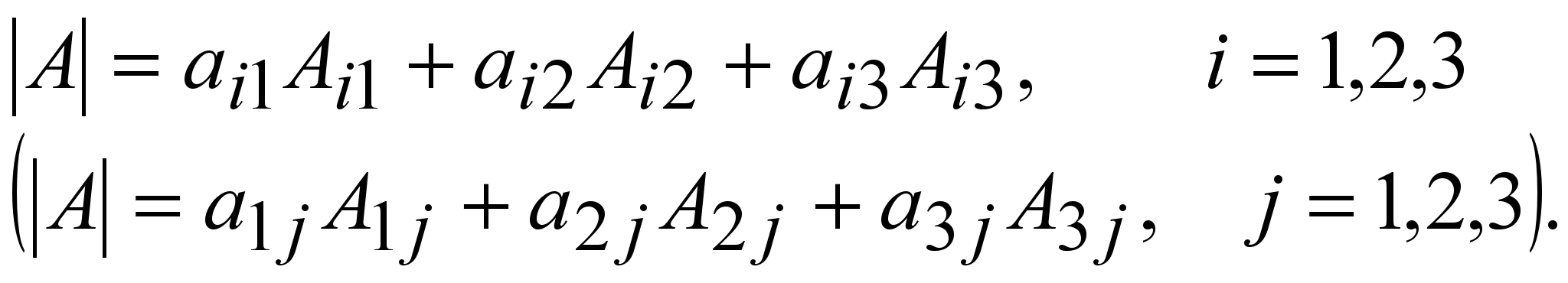(1.16)
Бұл теңдіктерді анықтауышты кез келген i-жол (j-баған) элементтері бойынша жіктеу немесе үшінші ретті анықтауыш үшін Лаплас формуласы деп аталады.
М.5*.
анықтауышын
3-баған
элементтері бойынша жіктеп, Лаплас
формуласы бойынша есептейік.
Шешуі. Жоғарыдағы (1.16) формуланы қолданыу арқылы
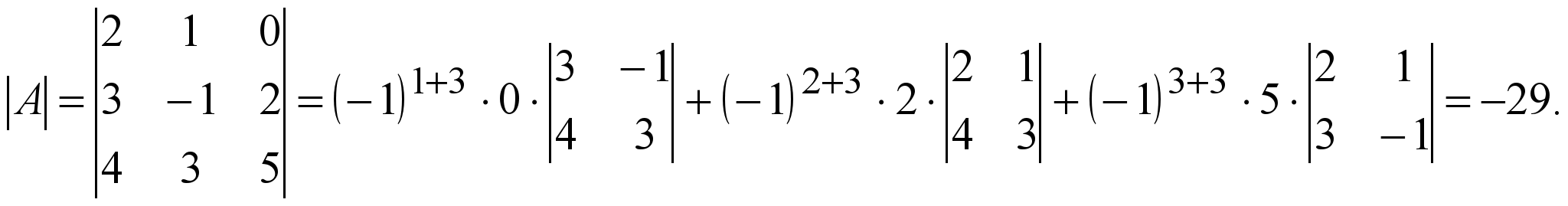
9 o . Анықтауыштың кез келген жолының (бағанының) элементтері мен басқа жолдың (бағанның) сәйкес элементтерінің алгебралық толықтауыш-тарына көбейтінділерінің қосындысы нөлге тең,
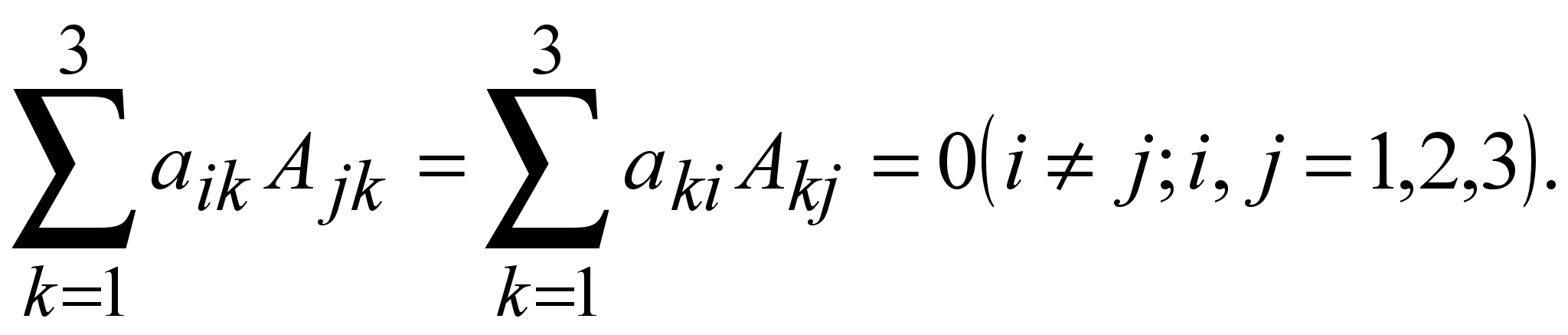(1.17)
Ескертулер. 1
o
.
Егер
n-ретті
шаршы матрица
болса, онда оған
анықтауышы сәйкес келеді және ол
n-ретті
анықтауыш
деп аталады.
2 o . Осы n ретті анықтауышты есептеу үшін,
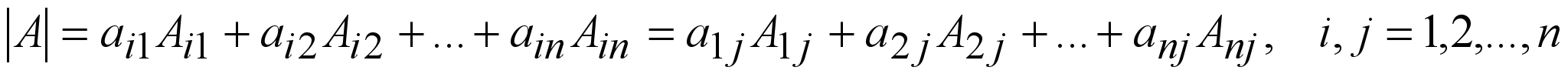(1.18)
Лаплас формуласын пайдалану арқылы, біртіндеп оның ретін бірге төмендете отырып, өзімізге белгілі болған үшінші немесе екінші ретті анықтауыштарға келтіріп, оның мәнін аламыз.
Енді n-ретті анықтауышты есептеудің басқа жолын көрсетейік. Ол үшін инверсия (ретсіз) деген ұғым енгізейік. Инверсия деп, (i 1 ,i 2 ,i 3 ,···,i n ,) сандарының орналасуындағы, үлкен санның кіші санға қарағандағы сол жағына, нешеуінің орналасу санын айтамыз. Мысал үшін, {3,5,2,4} сандар жиынтығын қарастырайық. Бұл орналасуда, 2 санының сол жағына 3 және 5 − екі сан, ал 4 санының сол жағына жалғыз ғана 5 саны орналасқан. Демек, инверсия саны 3-ке тең. Егер орналасу кезінде инверсия саны жұп болса, онда жұп орналасу, ал инверсия саны тақ болса, тақ орналасу деп аталады.
Сонымен, n-ретті A матрицасының анықтауышы деп, әр жол мен әр бағаннан тек бір-бір элементтен және мүмкін болған барлық элементтердің сәйкес таңбалармен алынған көбейтінділерінің алгебралық қосындысын айтамыз. Демек, әрбір қосылғыштың таңбасы орналасу кезіндегі көбейтінділерді құрайтын a ij элементтерінің төменгі индекстерінің арасындағы инверсия санына байланысты, яғни инверсия саны жұп болса − "+", тақ болса − "−" таңбасы алынады.
Ендеше анықтама бойынша:
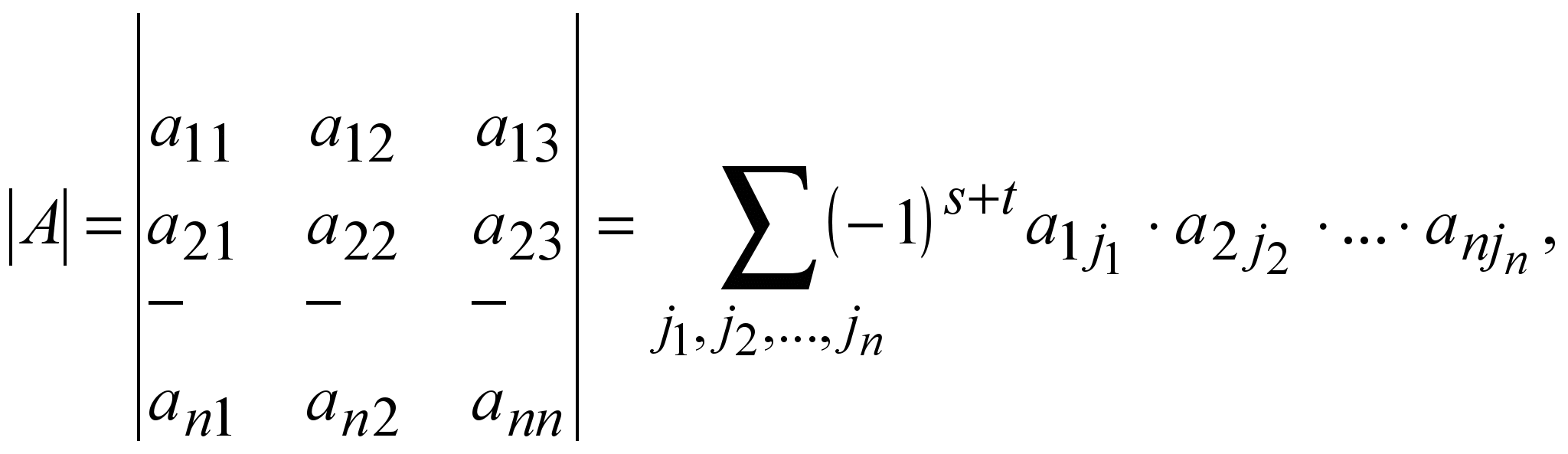(1.19)
Мұндағы s – бірінші i 1 ,i 2 ,···,i n , индекстер орналасуындағы инверсия саны; t – екінші j 1 ,j 2 ,···,j n индекстер орналасуындағы инверсия саны. Ал қосынды i 1 ,i 2 ,···,i n және j 1 ,j 2 ,···,j n индекстерінің 1,2,···,n – n санынан тұратын мүмкін болатын орналасулар үшін толық қамтылады.
3 o . Жоғарыдағы n-ретті анықтауыштар үшін, келтірілген 3-ретті анықтауыштың барлық қасиеттерін атап өтуге болады. Сондықтан да, оларды қайталап жатудың қажеті жоқ.
М.6*.
Үш бұрышты
матрицасына сәйкес
|A| анықтауышын есептейік.
Шешуі. Ол үшін (1.19) Лаплас формуласын қолданамыз
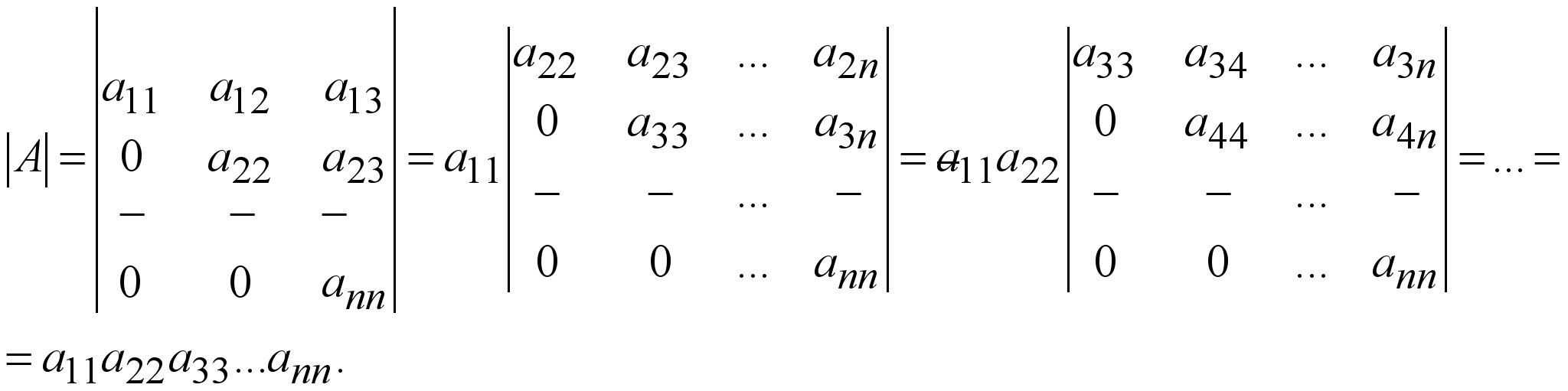
Бұл көбейтінділерде бірінші және екінші индекстер орналасуындағы инверсия саны нөлге тең болғандықтан "+" таңбасын аламыз. Ал анықтауыш мәнінің таңбасы бас диагональ бойындағы элементтер таңбаларының көбейтінділеріне байланысты болады.
